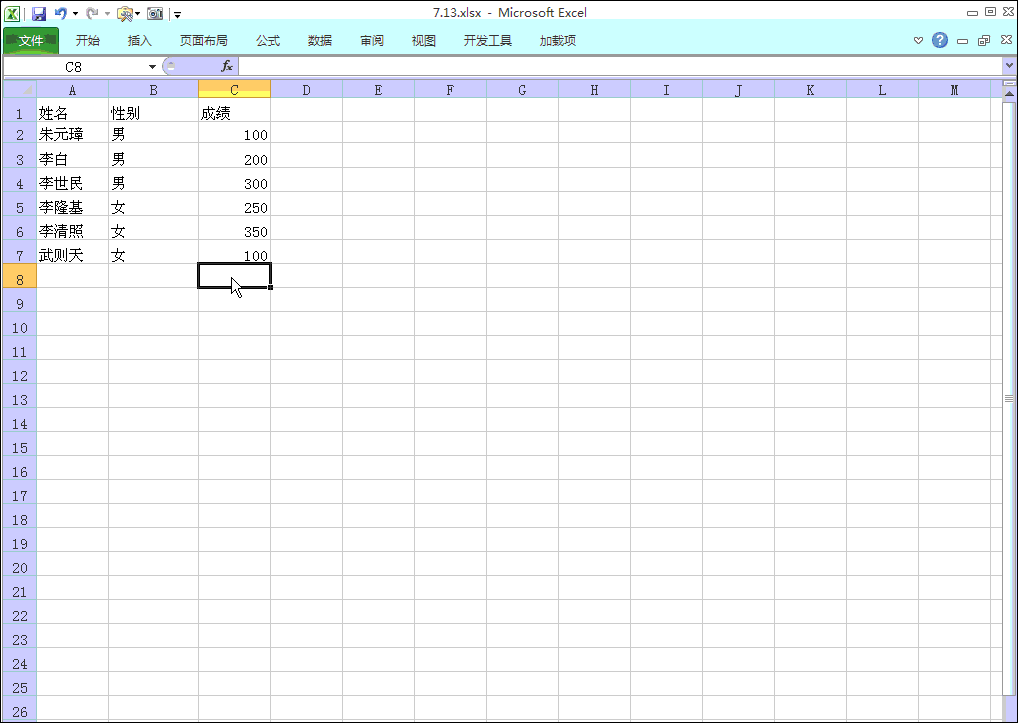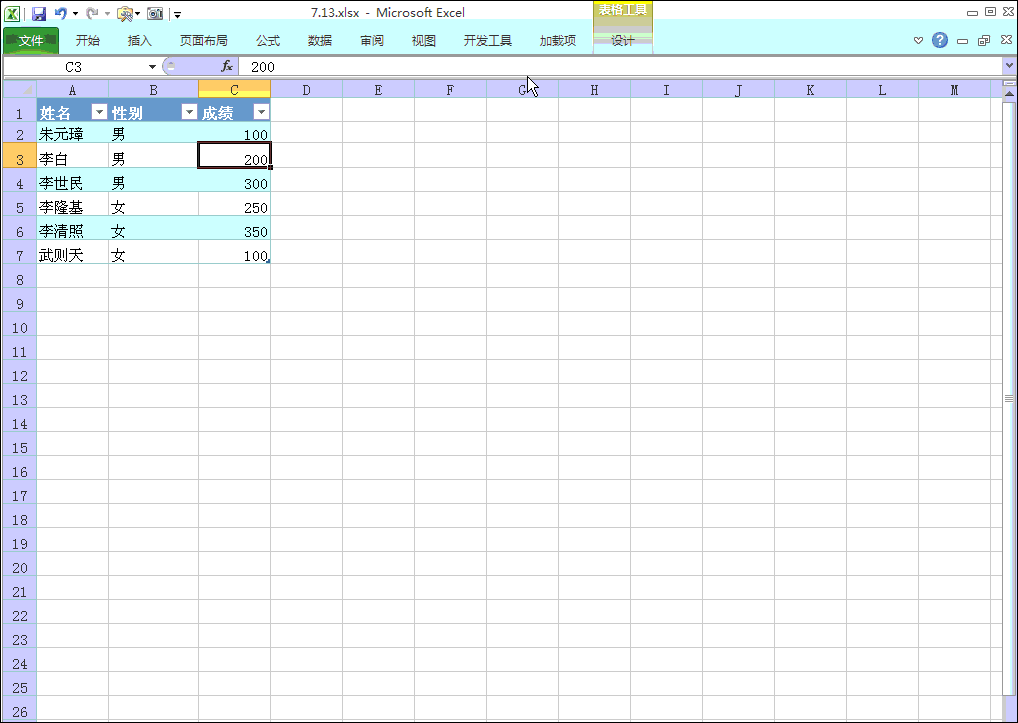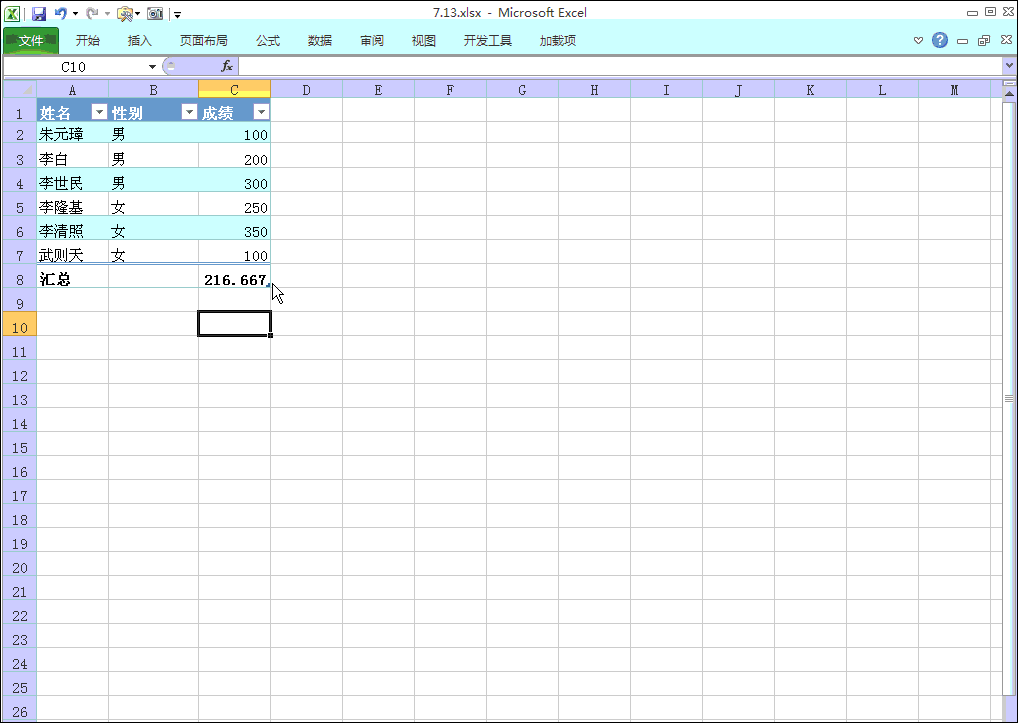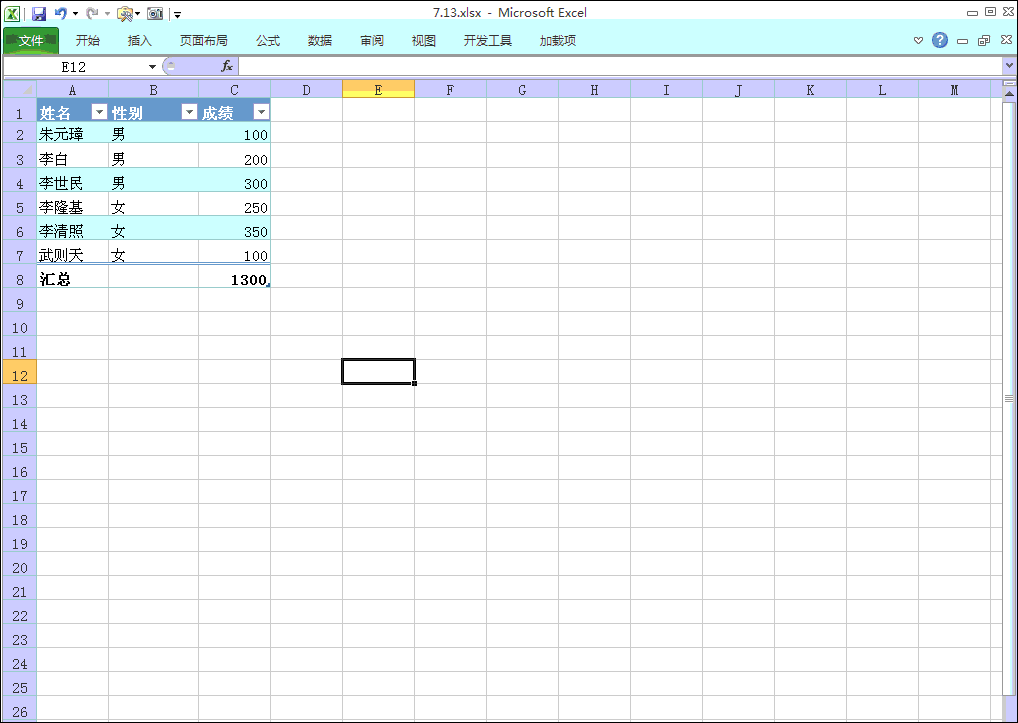
前面我们介绍了从少量样本中挖掘重要信息的内容,今天介绍的是大家日常使用的数据统计中最有代表性的是“平均值”。大概每个人从孩提时代起,关于身高、体重、体能测试、考试成绩等,都会把平均值作为参照标准进行比较吧!长大成人以后,关于工资、奖金等,也都会把自己所处的位置与总体平均值进行比较分析吧!公司预测营业额和生产量的需求,同样需要从历史数据的平均值中计算出来。例如,“出牛率1.28人”就是根据平均值导出的数据。一句话,平均值无处不在。
最优生产计划
在Excel中,有一个规划求解工具,这样我在工作生产中将得到很大的帮助,今天我们根据规划求解来计算出一个工厂的最优生产计划。 在原材料和电力等资源的限制下,为了实现最大利润,需要做出“最优生产计划”,此时就要使用规划求解。 用数学公式表达这个问题,如下所示(使用数学公式是为了方便说明,其
首先,举一个具体例子。假设屋里有10个人,而且知道所有人的平均身高,请你蒙上眼睛预测每个人的身高。怎样预测才能得到误差最小的数值呢?你肯定把平均值作为标准进行同答吧!因为这样可以避免出现大幅差异,降低危险性。平均值凝聚了整个团体的特征,利用平均值可以预测总体数值。平均值是日常生活中最常用的统计数值。“计算总体平均值,与此作比较,进行检验”,然后“作为预测材料灵活使用”,也是一种数据挖掘的方法。
求最优回归方程
我们应该求解只使用对目标变量真正产生影响的因子的回归方程。这是因为如果使用对目标变量不产生影响的因子,可能导致预测精确度降低。如果因子很少,求解的变量也就很少。这样,统计的变景数据很少,就可以节省时间,在实际应用中非常有效。在统计学上,仅仅使用产生影响的因子的方程叫做“最优回归方程”,或者&ld